Understanding Latent Variable Models in Image Analysis

Overview of LVM in Image Analysis 

When comparing our results with others and working with high-dimensional and correlated data, using Latent Variable Models (LVMs) has advantages. All these models go with the central idea that there are hidden or what are called ‘’Latent’’ variables, which could prompt the variability observed in the data. Thus, the presence of such LVMs helps uncover such structures and, as a result, makes a given context more interpretable by its users, whether they be academic researchers or business practitioners. This is especially the case in disciplines like psychology, finance, or biomedical research, in which detail can hide the signal. Therefore, through LVMs, analysts can abstract huge quantities of information into more easily understood forms to make better sense of them and hence provide better inputs into decision-making.

The computer vision based technology that detects and analyzes human posture. Taken From Article, Human Pose Estimation for Sport Analytics

There are numerous approaches to LVMs, and all are generally suited to certain data types and forms of analysis. Examples of LVMs include Principal Component Analysis (PCA), Factor Analysis, and Autoencoders to show how LVMs retain vital data characteristics while minimizing the dimensionality.

For example, it uses PCA to transform two correlated variables into two principal components, which makes analysis easier without considerable loss of information. Similarly, Autoencoders reduce data size to a latent space where data is easily reconstructible and filtered from noise. Consequently, LVMs may improve the capability of facial recognition systems and accelerate the usage of medical imaging diagnostics. By incorporating these models, researchers can comprehensively discover the hidden potentials and novelties needed for their research domain improvements. 

What Are Latent Variable Models? 

Latent Variable Models are statistical models that postulate the presence of unmeasured and, therefore, not directly observed variables called latent variables. These hidden variables are useful to explain relationships and associations between the variables observed, making it easier to understand the process occurring behind all the measured variables. 

The concept can be summarized as follows: 

• Latent Variables: These are not directly measured but are inferred from the observed data. They represent underlying factors or constructs that influence the data. 

• Observed Variables: These are the measurements or data points collected in a study. 

The primary goal of LVMs is to reduce dimensionality, identify structure, and improve interpretability in complex datasets. 

Face Recognition uses computer algorithms to find details about a person's face. Taken From the Article, Face Recognition and Detection

How Are Latent Variable Models Useful? 

1. Dimensionality Reduction: LVMs are effective in slightly reducing the number of variables but, more importantly, retaining the key information. This is especially important with high-dimensional data, where more conventional paradigms could fail to produce usable results.  

2. Dealing with Correlated Predictors: Quite often, datasets contain predictors that are correlated with each other, which can make analysis difficult. LVMs like PCA and PLS produce latent variables that are orthogonal to each other, which makes modelling easier.  

3. Uncovering Hidden Structures: Through such modelling, researchers can capture relations that might not be known from the raw data on the table. This is especially useful when performing EDA Exploratory Data Analysis.  

4. Improving Predictive Models: For this reason, when predictive models' value is based on the work of latent variables, it is possible to achieve a better analysis of data points than traditional statistical techniques.  

5. Enhancing Interpretability: LVMs prescribe how relationships among the variables can be viewed or measured. For example, in a psychology study, the latent exogenous variables could refer to concepts such as intelligence or motivation. 

The Role of Latent Variables in Image Analysis 

• Feature Extraction: LVMs can extract features in an image, including edge, texture, and shape features. This process assists in dimensionality reduction while retaining important information.  

• Dimensionality Reduction: Pictures very often include an enormous volume of information. Otherwise, the subsequent analysis is more manageable because LVMs map the high-dimensional pixel data to a lower-dimensional space.  

• Understanding Relationships: When using CLA to model latent variables, it becomes easier to determine associations between different images, such as colour, texture, and shape, since the results are less ambiguous. 

How Latent Variable Models Work in Image Analysis 

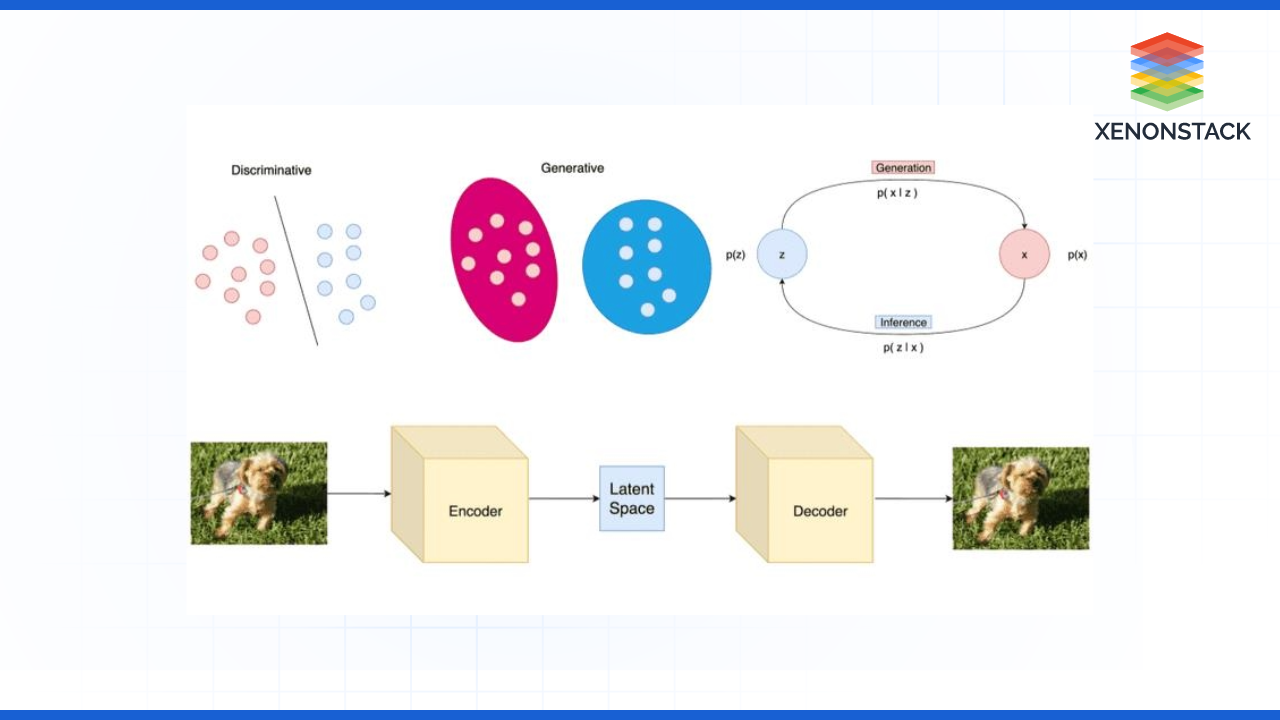
Fig – High-level architecture of LVM 

Understanding the Concept of Latent Variables 

• Latent Variables: These are unobserved factors that influence the observed data. In image analysis, they could represent features like shapes, colours, or textures that are not directly measurable but affect how we perceive the image. 

Data Representation 

• High-Dimensional Data: Images are typically represented as high-dimensional data, with each pixel contributing to the overall representation. For example, a 100x100 pixel image has 10,000 dimensions (one for each pixel). 

• Dimensionality Reduction: LVMs aim to reduce this complexity by identifying a smaller set of latent variables that capture the essential features of the images. 

Common Techniques Used 

• Eigenvalue Decomposition: Currently, PCA operates by computing the covariance between the image data and then obtaining its eigenvalues and eigenvectors. The first few eigenvectors (principal components) associated with high eigenvalues include a substantial proportion of the variance.  

• Transformation: The original image data is mapped on the subspace determined by these principal components, obtaining fewer dimensions while preserving the most important features.  

• Architecture: The autoencoder comprises two subsystems: the encoder, which encodes the input image into a latent representation (pure code), and the decoder, which maps the code into a reconstructed image.  

• Training: To let the model learn meaningful features in the latent space, the model is trained in such a way that it has to reconstruct the images as closely as possible with the original one.  

• Probabilistic Approach: In contrast to the ones mentioned before, VAEs consider that the latent variables are distributed according to a certain probability distribution (Gaussian, for example). This also makes it possible to create new images by creating them out of the latent space.  

• Inference: The model employs methods like the reparameterization trick, which allows it to perform inference and training in a single pass. This trick teaches the model to estimate the distribution of the variables in the latent space.  

• Two Networks: Specifically, it has a generator that produces images and a discriminator that assesses and criticizes them. The generator, on the same note as the training data, learns how to create images that can pass through the discriminator’s feedback to output a favourable result.  

• Latent Space Control: The generator trains on noise vectors derived from a latent space to generate variety while enabling the control of attributes in the generated images.

Application Workflow 

• Preprocessing: Images are preprocessed (e.g., resized, normalized) to prepare them for model training. 

• Model Selection: Choose an appropriate LVM based on the specific task (e.g., PCA for dimensionality reduction, autoencoders for denoising). 

• Training: The chosen model is trained on a dataset of images. During training, the model learns to identify and encode latent variables. 

• Feature Extraction: After training, the latent representations can be extracted for analysis or further processing. 

• Inference: The model can be used for tasks like generating new images, classifying images, or detecting anomalies based on the learned latent variables. 

Evaluation and Interpretation 

• Reconstruction Error: For autoencoders and VAEs, the reconstruction error helps evaluate how well the model has learned the underlying structure of the data. 

• Visualization: Latent spaces can be visualized (e.g., using t-SNE or PCA) to understand how images cluster based on their latent representations. 

• Performance Metrics: For tasks like classification or anomaly detection, standard metrics (accuracy, precision, recall) are used to assess model performance.